La compression des données

Sur des réseaux à haut débit (Fibre, Ethernet, WiFi) on envoie généralement les données de la manière la plus pratique à manipuler. Souvent, on choisit même un format qui facilitera la compréhension par l’humain en cas de problème. Ce choix a un coût en taille des données, qui pose peu de problèmes sur les réseaux à haut débit.

Mais sur un réseau à faible débit comme LoRaWAN, il devient impérativement nécessaire d’envoyer ses données de la manière la plus économe possible en bande passante.

Pour ce faire, il existe deux techniques : le bit packing (litt. l’empaquetage de bit) et la compression proprement dite.

Bit packing

Il est habituel en informatique d’organiser les données sous forme d’octets ou de groupes d’un multiple de 2 d’octets, c’est-à-dire dans 8, 16, 32, 64, 128 bits, etc…

Ainsi, on emploiera 8 bits pour représenter des nombres entre 0 et 255 ou entre -128 et +127, 16 bits pour des nombres entre 0 et 65535 ou entre -32768 et +32767. Lorsqu’on veut que les données soient immédiatement lisibles par des humains, on emploie des caractères, c’est-à-dire généralement 8 bits par chiffre. Il faut alors 16 bits pour représenter des nombres entre 0 et 99 ou entre -9 et +9, 24 bits pour représenter des nombres entre 0 et 999 ou entre -99 et +99, etc…

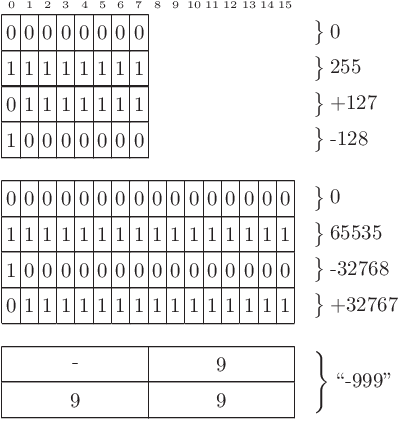
On voit que la représentation humainement lisible coûte environ le double d’une représentation en octets, mais même l’emploi d’octets peut amener à gaspiller. Prenons l’exemple d’une suite de 4 nombres entre 0 et 1000 (appelons-les A, B, C et D). Chacun peut être représentés sur 10 bits. Si on emploie des entiers de 16 bits, les 4 nombres prendront 8 octets au total. Mais si colle bout à bout les groupes de 10 bits, on peut les faire tenir dans 5 octets.

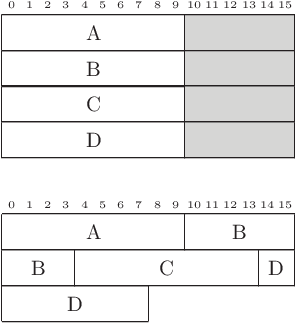
Cette technique du bit packing peut également être employée pour une suite de nombres de tailles variées.

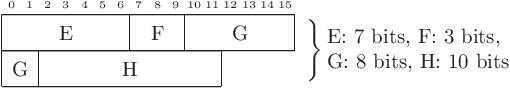
Compression

Le but de la compression est de réduire la taille des données au-délà du bit packing, en s’appuyant sur les redondances au sein des données. Par exemple, si on veut envoyer 1001, 1002 et 1003, on pourrait les résumer en 1000, 1, 2 et 3. L’important est de trouver une manière de formater les données qui tire partie de cet allègement sans nécessiter un surplus de données qui le contrecarre.

Compression manuelle

Prenons un exemple concret, où l’on veut envoyer une série d’entiers. On va choisir d’envoyer deux types de messages, en tirant parti du bit packing. Le type est indiqué par le premier bit.

Le premier type, qu’on appellera non compressé, est composé d’un bit de valeur 0 puis d’un nombre sur 7 bits (K), qui indique le nombre d’entiers de 16 bits qui suivent. Un message LoRaWAN ne peut jamais dépasser 222 octets, donc on ne pourra pas avoir plus de 110 entiers. Or 7 bits sont suffisants pour représenter des nombres de 0 à 128.

Le deuxième type, qu’on appellera compressé est composé d’un bit de valeur 1 puis d’une taille d’entier sur 4 bits (T) et d’un nombre d’entiers sur 10 bits (K) qui suivent un premier entier de 16 bits (B). Pour s’aligner sur les octets, on rajoute un bit inutilisé dont la valeur est 0. La taille des entiers est codée sur 4 bits pour représenter des nombres de 1 à 15 (puisqu’on va employer des tailles plus petites que dans un message non compressé, où ils font 16 bits). Le nombre des entiers est codé sur 10 bits pour représenter des nombres de 1 à 1023 (puisque le nombre maximal d’entiers, s’ils font 2 bits, sera de 872).

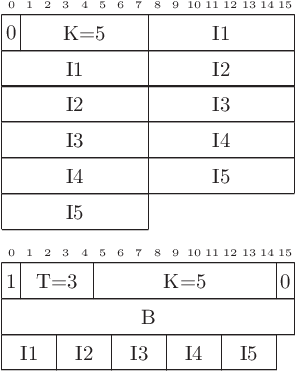
Avec K=5 et T=3, le message non compressé fait 11 octets et le message compressé 6 octets.

Compression automatique

Quand les données font une certaine taille, les algorithmes de compression sont capables de faire ce travail automatiquement. L’algorithme DEFLATE, par exemple, employé par l’utilitaire gzip, va transformer 250 octets aléatoires en 200 à 280 octets, selon la proximité des octets entre eux.

Il est nécessaire de tester les différents algorithmes de compression pour vérifier quelles seront leurs efficacités respectives sur les données qu’on souhaite envoyer.

Une des approches est d’augmenter la taille des données qu’on fournit à l’algorithme de compression. DEFLATE, toujours lui, va transformer 3 Ko aléatoires en 2 à 2,7 Ko, selon la proximité des octets entre eux. Donc au lieu d’envoyer les données de manière la plus fréquente possible, on peut attendre d’avoir une masse critique de données, puis la comprimer et faire une longue salve de messages qui, mis bout à bout, contiennent cette masse de données comprimée.